Utilidad Cardinal

Como se mencionó con anterioridad, en el pasado algunos economistas proponían que la utilidad podía medirse asignándosele una medida, los “útiles”. Así, sostenían que a las acciones que causaban placer se les podía asignar un número positivo y a las acciones que provocaban un mal o dolor, se les asignaba un número negativo, y por último se sumaban algebraicamente estos números. Además, se proponía que estas medidas podían obtenerse para cada una de las personas que era afectada por las acciones en juego, es decir, que la utilidad era susceptible de ser medida cuantitativamente y comparable interpersonalmente.
El desarrollo de una función de utilidad cardinal facilita la comprensión de los conceptos de utilidad total y utilidad marginal. Si se observa la Figura 1, se puede apreciar, cómo la utilidad total aumenta a medida que se consumen unidades adicionales del bien bajo estudio, mientras que la parte inferior de la figura muestra cómo el incremento de utilidad que proporciona cada unidad adicional del bien en cuestión es cada vez menor, a medida que el consumo aumenta. La función que vemos en la parte superior es la utilidad total, mientras que la parte inferior muestra el comportamiento de la utilidad marginal.

​​

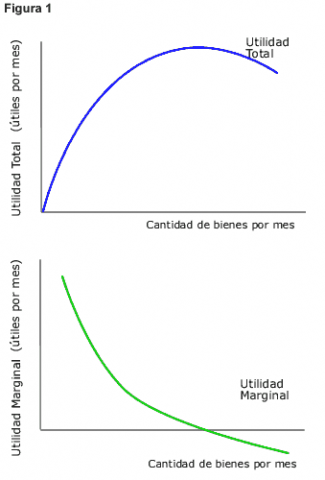
Traducido en otros términos, estas funciones estarían mostrando que las primeras unidades consumidas, proporcionan al individuo mayor placer que las últimas, a medida que éste va alcanzando un punto de saciedad. Es decir, cada unidad adicional que se consume brinda una utilidad menor que la anterior, esto es lo que se denomina utilidad marginal decreciente.

En términos matemáticos podemos decir que la primera derivada de la función de utilidad es positiva, mientras que la segunda es negativa.

De todas formas, pasaremos a continuación a indagar en el análisis de la utilidad ordinal, que puede darnos mayores instrumentos para estudiar el comportamiento de elección del consumidor.

Utilidad Ordinal

El enfoque de la utilidad ordinal es menos rígido, y consiste simplemente en ordenar los niveles de utilidad. Cuando se hace referencia a “utilidad” en términos ordinales, se quiere reflejar solamente el ordenamiento de las preferencias. Se define entonces a utilidad como una variable cuya magnitud relativa indica el orden de preferencias.

El instrumento que utilizamos en este análisis se denomina curva de indiferencia y surgen de una función de utilidad un poco más compleja. Tenemos así, la Figura 2 para dos bienes X e Y, que describe una función de utilidad cardinal U(x, y), la utilidad total se mide en la tercera dimensión. Si tomamos la cesta x= x1, y= y2, la utilidad total viene dada por el segmento T T´. Si mantenemos la cantidad de uno de los bienes constante, vemos como la utilidad total aumenta a medida que la cantidad del otro bien se incrementa. Esto se puede observar en el segmento VBG para y constante igual a y3 y en el segmento ARUG para la cantidad del bien x igual a x2.

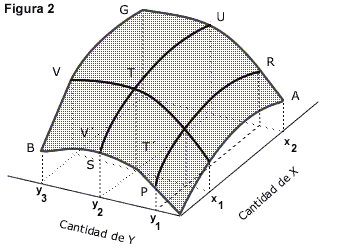
Las utilidades marginales de cada cesta, respecto a cada uno de los bienes se miden por las derivadas parciales de la función de utilidad total respecto a x o a y.

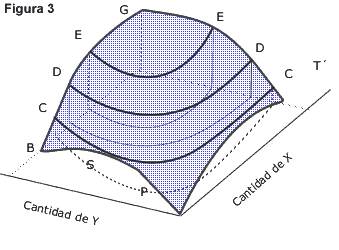
En la Figura 3 vemos la misma función de utilidad total, con la diferencia de que ahora se resaltan los puntos que unen segmentos de igual altura, es decir aquellas cestas de consumo que representan la misma utilidad para el consumidor. Estas curvas de utilidad constante, son las curvas de indiferencia. En otras palabras, cualquier cesta de consumo ubicada sobre una de esas curvas proporciona al consumidor la misma utilidad, por lo tanto es indiferente al elegir cualquiera de ellas.