Las curvas de indiferencia son un conjunto de combinaciones de bienes que proporcionan la misma utilidad al consumidor. Sobre una curva de indiferencia el consumidor es indiferente entre cualquiera de las canastas de bienes que se le presentan. Si representamos las curvas de indiferencias en dos dimensiones obtenemos la Figura 4.

​​

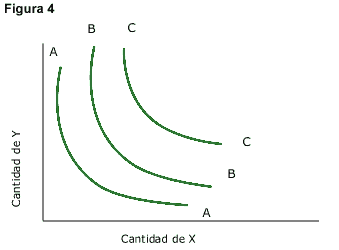
Las curvas de indiferencia regulares poseen las siguientes características:

• Tienen pendiente negativa

Se supone que si hablamos de cestas de dos bienes, siempre más es preferible a menos. Es decir, si tenemos una cesta de bienes (x1, y1) y otra cesta (x2, y2) tal que la segunda contiene la misma cantidad de uno de los bienes y más de uno de ellos, la segunda cesta será preferida a la primera. Este supuesto se denomina “preferencias monótonas”. Este supuesto de preferencias monótonas implica que las curvas de indiferencia tienen pendiente negativa. Miremos la Figura 5 si partimos de la cesta (x1, y1) y nos desplazamos en sentido ascendente y hacia la derecha, nos encontraremos sí o sí en una cesta preferida. En cambio si nos movemos hacia abajo y a la izquierda, necesariamente estaremos en una situación peor. Por lo tanto, para encontrar una situación indiferente, debemos movernos o bien, hacia arriba a la izquierda o bien, hacia abajo a la derecha, por lo tanto la curva debe tener pendiente negativa.

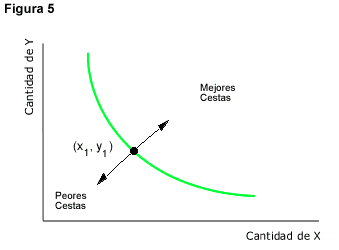
• Las curvas de indiferencia no se cortan entre sí.

Supongamos tres cestas de consumo, A, B y C, tales que A se encuentre en una de las curvas, B sobre la otra curva y C en la intersección de ambas, como vemos en la Figura 6.  Partimos del supuesto de que las curvas de indiferencia allí dibujadas representan distintos niveles de utilidad, por lo que una de las cestas, por ejemplo la A es preferida a la B. Según la definición de curvas de indiferencia, sabemos que la cesta A es indiferente a la C y que la cesta C es indiferente a la cesta B. Si utilizamos el supuesto de transitividad, deberíamos obtener que las cestas A y B sean indiferentes. Pero como habíamos supuesto al principio A es preferida a B, con lo que demostramos que las curvas de indiferencia que representan distintos niveles de utilidad, no pueden cortarse.

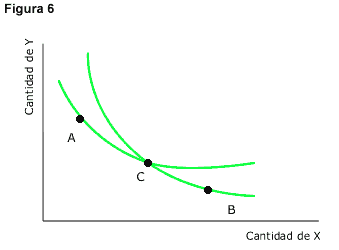
• Son convexas al origen.

Esto es lo mismo que decir que se prefieren las cestas medias a las cestas con combinaciones extremas (nada de un bien y todo del otro bien). Una curva es convexa al origen cuando la línea que conecta dos puntos de la curva pasa por encima de la curva de indiferencia. Este supuesto no puede demostrarse desde los supuestos de las preferencias, sino que se basa en el principio de la diversidad en el consumo.

Este supuesto es útil en el sentido de encontrarnos con curvas de indiferencia que impliquen que el consumidor preferiría especializarse en el consumo de uno de los dos bienes. Estos son casos de estudio particulares. El caso de estudio general se refiere a aquel en que el consumidor desea intercambiar una parte de uno de los bienes por una parte del otro y terminar consumiendo una cierta cantidad de cada uno más que especializarse en el consumo de alguno de los dos.
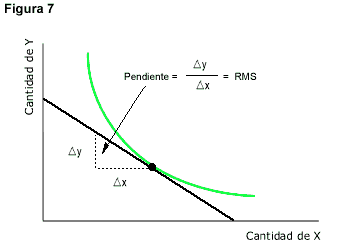
La relación marginal de sustitución

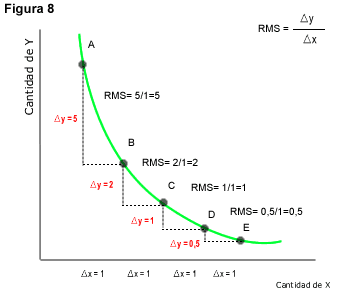
Técnicamente, la relación marginal de sustitución (RMS) es la pendiente en un punto de la curva de indiferencia. La RMS mide la relación a la que el consumidor está dispuesto a intercambiar, o sustituir, el consumo de un bien por el otro. En la Figura 8 podemos ver cómo varía la RMS a medida que nos movemos a través de los puntos de la curva de indiferencia. Si comenzamos a movernos desde el punto A, vemos que el consumidor está dispuesto a sacrificar 5 unidades de y por una unidad adicional de x; para pasar del punto B al C, nuestro consumidor está dispuesto a renunciar al consumo de 2 unidades de y por una unidad más de x. Ahora bien, si el le preguntamos al consumidor cuánto daría por una unidad más del bien x, lo que implica pasar al punto D, este renunciaría a solamente una unidad de y. Es decir, a medida que nos movemos hacia la derecha, la RMS de x por y disminuye. Esta propiedad se conoce como tasa marginal de sustitución decreciente.

Distintos tipos de curvas de indiferencia

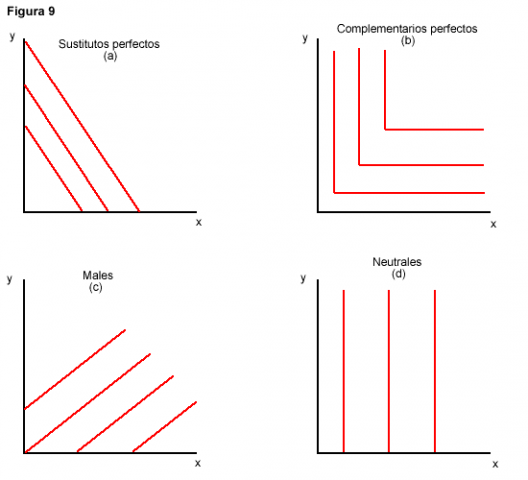
En la Figura 9 podemos observar distintas formas de curvas de indiferencia, estas curvas reflejan diferentes preferencias por los bienes. En la primera figura (a) observamos curvas de indiferencia para bienes que el consumidor considera como sustitutos perfectos, la RMS es constante a lo largo de toda la curva. Cualquiera de los dos bienes satisface igualmente la necesidad del consumidor.

En la figura (b) se presentan curvas de indiferencia de bienes que son complementarios perfectos y se consumen en proporciones fijas. Estas curvas indican que aunque la cantidad de uno de los bienes aumente, si la cantidad del otro bien se mantiene constante, la utilidad del individuo no se modifica. Por ejemplo los pares de zapatos, si aumenta la cantidad de zapatos del pie izquierdo, sin que se modifique la cantidad de zapatos del pie derecho, la utilidad que obtiene el individuo permanecerá constante.

En la figura (c) tenemos el caso de un mal y un bien. Un mal es una mercancía que no le agrada al consumidor. Sobre el eje y se mide la cantidad del “mal” y sobre el eje de las x se mide la cantidad del producto que le agrada al consumidor. Las curvas de indiferencia tienen pendiente positiva debido a que si queremos que el consumidor acepte una unidad adicional del producto que no le agrada, deberemos entonces, compensarlo con una mayor cantidad del producto que si le agrada para que se mantenga sobre la misma curva de indiferencia. Supongamos que al consumidor le agradan las bebidas colas pero no le gusta beber agua mineral, entonces si queremos que el consumidor acepte un vaso adicional de agua, deberemos compensarlo con una cantidad mayor de bebida cola para que se mantenga sobre la curva de indiferencia.

Por último la figura (d) muestra el caso en que el bien que se mide en el eje y se considera neutral. La utilidad del sujeto no varía según la cantidad del bien y que consuma, su utilidad sólo depende de la cantidad de x que consume. Cuanto más tenga de x mejor, sin importar la cantidad de y.